The Ideal Gas Law, pV=nRT, is such a famous and fundamental equation that it is always taught in the first lesson of gasometry. Involving only four variables, T (temperature), p (pressure), V (volume), and n (amount of substance), the equation is simplistic in comparison to the complexity and uncertainty of gases it tries to describe. Simple as it is, however, Ideal Gas Law is not the conclusion of one single scientist. Experts in chemistry and physics took over two hundred years to study the properties of gases and eventually came up with this equation as a collaborative effort.
Boyle’s Law
The history of Ideal Gas Law started with British physicist Robert Boyle’s experiment in the mid-17th century. In the experiment, Boyle poured mercury from one side of a closed J-shaped tube, which forced the air on the other side to compress. He measured the volume of air and the difference between mercury columns, as illustrated below. After conducting multiple trials with varied quantities of mercury, he discovered that, under controlled conditions, a gas's pressure is inversely proportional to its volume. Boyle concluded his observation with a mathematical formula called Boyle’s Law: When T and n are constant, pV=k. His findings determined the left side of the Ideal Gas Law.
Gay-Lussac’s Law
While Boyle’s Law focused on the relationship between pressure and volume, French chemist Joseph Louis Gay-Lussac studied the correlation of volume and temperature. In the late 18th century, they discovered that under low pressure, the expansion rate of any gas is a linear equation of temperature in degrees Celsius (℃). If the volume of a certain gas in boiling water (100℃) is V100 while V0 in ice water (0℃), Gay-Lussac found out that the gas always increased its volume by 37% from 0℃ to 100℃.
To extend the equation to a broader range, we use Vt to replace V100.
Gay-Lussac then described the relationship between volume and temperature: When pressure is constant, every 1℃ increase in temperature of a certain gas will expand its volume by 1273 of its volume at 0℃. Familiar with the number “273”? Yes, Gay-Lussac’s Law helped physicist Lord Kelvin to determine the famous “absolute zero”. Over a century later, after Kelvin temperature was proposed, Gay-Lussac’s Law was eventually expressed in a similar equation as Boyle’s Law.
Clapeyron’s Law
Coming to the mid-19th century, French chemist Clapeyron combined Boyle’s Law and Gay-Lussac’s Law, expressing p, V, and T in one equation. The initial state of a certain gas is p1, V1, T1 and the final state p2, V2, T2.
Using Boyle’s Law, we know:
Using Gay-Lussac’s Law we know:
Substituting V’ with equation 2, we get the Clapeyron’s Law:
Rearranging Clapeyron’s Law, we find a similar equation to the Ideal Gas Law, pV=kT.
Later on, scientists further expressed the constant k with nR where R is the multiple of NAk, the Avogadro constant and Boltzmann constant and n is the mole mass of gases.
Conclusion
It took scientists more than two centuries of hard work to conclude a simple equation, the Ideal Gas Law. Next time when someone wonders why gasometry is not as complicated as it sounds, tell them about the long history behind it!
Reference List
Team, P. (2022). Boyle’s Law: Definition, Explanation, Applications. [online] PSIBERG. Available at: https://psiberg.com/boyles-law/ [Accessed 2 Mar. 2024].
Wikipedia Contributors (2024). Gas constant. [online] Wikipedia. Available at: https://en.wikipedia.org/wiki/Gas_constant [Accessed 2 Mar. 2024].
Wikipedia Contributors (2024). Boyle’s law. [online] Wikipedia. Available at: https://en.wikipedia.org/wiki/Boyle%27s_law [Accessed 2 Mar. 2024].
Wikipedia Contributors (2024). Ideal gas law. [online] Wikipedia. Available at: https://en.wikipedia.org/wiki/Ideal_gas_law [Accessed 2 Mar. 2024].
华彤文,王颖霞,卞江,陈景祖。(2013)。《普通化学原理》。第四版。北京大学出版社。
.png)



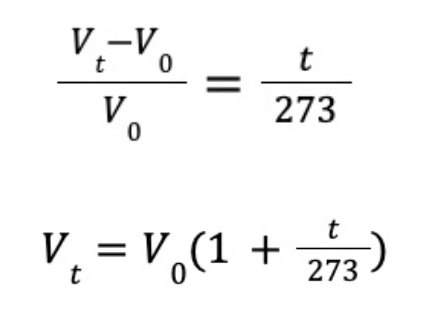




Comments