Moments, Center of Gravity, and Inertia

Figure 1: A Seesaw in Action 

Imagine you and your friend sitting on a seesaw (Ref. Figure 1). Almost certainly, someone would be dragged down and someone would be dragged up. This phenomenon is caused by the core physics principles of moments, center of gravity, and inertia! These concepts are crucial in mechanics, such as in rotational dynamics. 

Centre of Gravity

First, to introduce this fundamental concept, the center of gravity is the very center of this topic. 

The center of gravity is a singular point representing the point through which the weight of an object acts. This point is significant because it helps to analyze the forces and moments acting on the system. The center of gravity is determined mainly by the distribution of weight across the body. 

In simpler physics, the center of gravity is assumed to be the system's center-most point when the word “uniform” is included. For example, in a uniform seesaw of 5 meters in length, the center of gravity would be 2.5 meters away from either end. This is always assumed to be true unless stated otherwise. For 3-dimensional objects, it can be the center point of a sphere (Ref. Figure 2). 

Figure 2: Center of gravity of simple objects

However, for scenarios in non-uniform gravitational fields such as larger celestial bodies, the center of gravity will shift slightly towards the source of gravity due to the varying magnitudes of gravitational force acting on the object. For the moon, the center of gravity is leaned towards the Earth’s side as Earth is the source of gravity. For non-uniform objects, calculus can be used to integrate the volume or area of the object. 

Moments 

Wait a moment, how do moments relate then? 

A moment (also known as torque) in physics refers to the tendency of a force to cause an object to rotate about a specific point or axis. 

The moment is defined as the product of the force and the perpendicular distance between the force and the pivot point. The pivot point is a singular point on the body where the object rotates, such as a door hinge. 

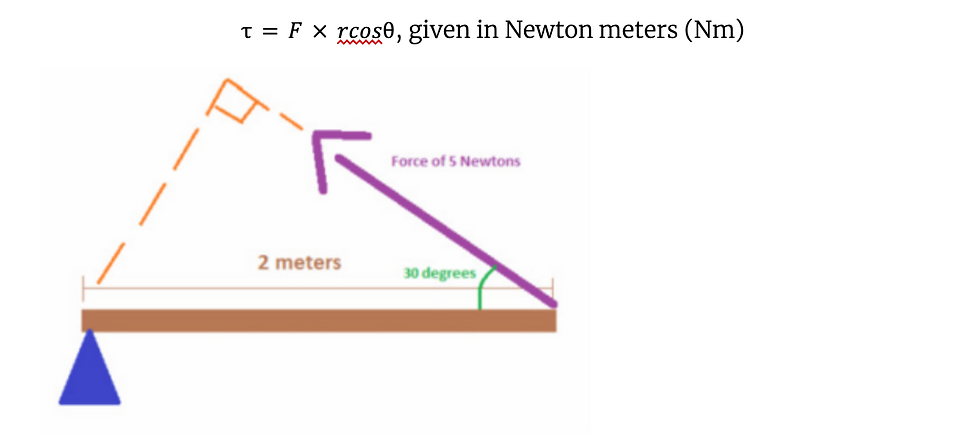
Figure 3: Worked Example

In this specific example in Figure 3, the moment will be: 

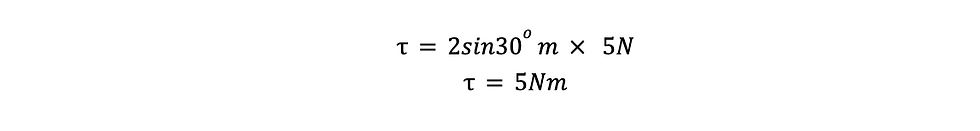
It is important to note that moments are for perpendicular distances, while the parallel distance is defined as work done. 

Moments work in terms of turning direction. Therefore, moments can only be defined as moving the body clockwise or counterclockwise (Ref. Figure 4). 

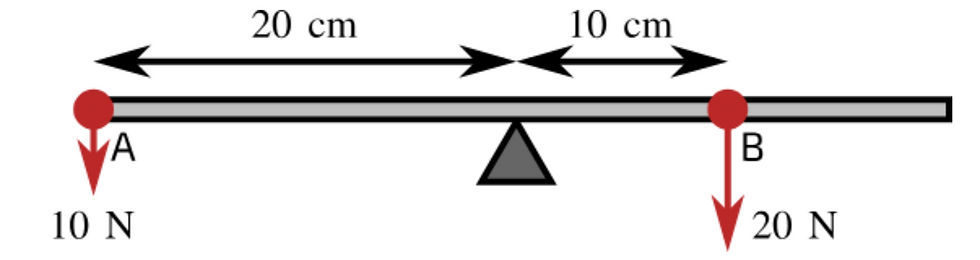
Figure 4: Demonstration of Moments 

In a balanced system with rotational equilibrium, the net moment must be 0, where the sum of the anticlockwise moments must equal the sum of the clockwise moments. So if the clockwise moment of the body is greater than the anticlockwise moment, the body will turn clockwise and vice versa. 

Moment of Inertia

The moment of inertia is described as the tendency of an object to rotate. It is a quantifiable measure of an object’s resistance to angular acceleration. 

The moment of inertia is affected by the mass distribution relative to the axis (shape). For example, a solid disk has a different moment of inertia compared to a hollow cylinder even if they have the same mass. 

To derive an object’s moment of inertia, the distance from the rotation squared will be integrated concerning the small mass element of dm. 

The moment of inertia can also be added up, but it can vary for different axes where the principal axes must pass through the center of mass. 

Interestingly, the moment  can also be represented as the product of the body’s moment of inertia I and the angular acceleration.

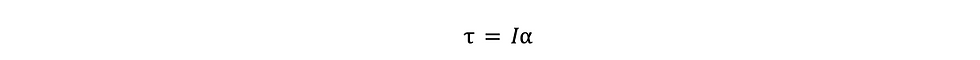
Applications 

1. Mechanical Engineering: Understanding how rotational dynamics work is crucial to understanding gears, flywheels, and anything related to spinning motion. 

2. Rotational dynamics is also an important method in analyzing safety in different spinnable objects, such as the design of a seesaw!

3. This concept can also be applied to sports sciences with tennis rackets and golf clubs! 

Fun Facts 

1. The center of mass is NOT equal to the center of gravity! 

2. French mathematician Pierre Varignon was the first person to discover the phenomenon of moments! 

3. The law of inertia was first formulated by Galileo Galilei and later generalized by Rene Descartes 

Works Cited 

BYJUS (n.d.). Centre of Gravity - Detailed Explanation, Calculation, FAQs. [online] BYJUS. Available at: https://byjus.com/physics/centre-of-gravity/.

Isaac Physics. (2024). Isaac Physics. [online] Available at: https://isaacphysics.org/pages/step_up_28_text [Accessed 15 Dec. 2024].

Luebkeman, C. (1998). What is a Moment. [online] web.mit.edu. Available at: https://web.mit.edu/4.441/1_lectures/1_lecture5/1_lecture5.html.

Physics Girl. (2024). Understanding Moment of Inertia in Physics: A Comprehensive Overview | Physics Girl. [online] Available at: https://physicsgirl.in/understanding-moment-of-inertia-in-physics/.

Quizlet. (2024). Seesaw Diagram. [online] Available at: https://quizlet.com/326679941/seesaw-diagram/ [Accessed 15 Dec. 2024].