A Mobius strip, also known as the Mobius band is a mathematical object/surface that can be formed by attaching the ends of a strip of paper together with a half-twist. The mathematical object challenges the concept of space and geometry. The shape appeared initially in Roman Mosaics in the third century CE, and the concept was later discovered in 1858 by German mathematician August Ferdinand Mobius.
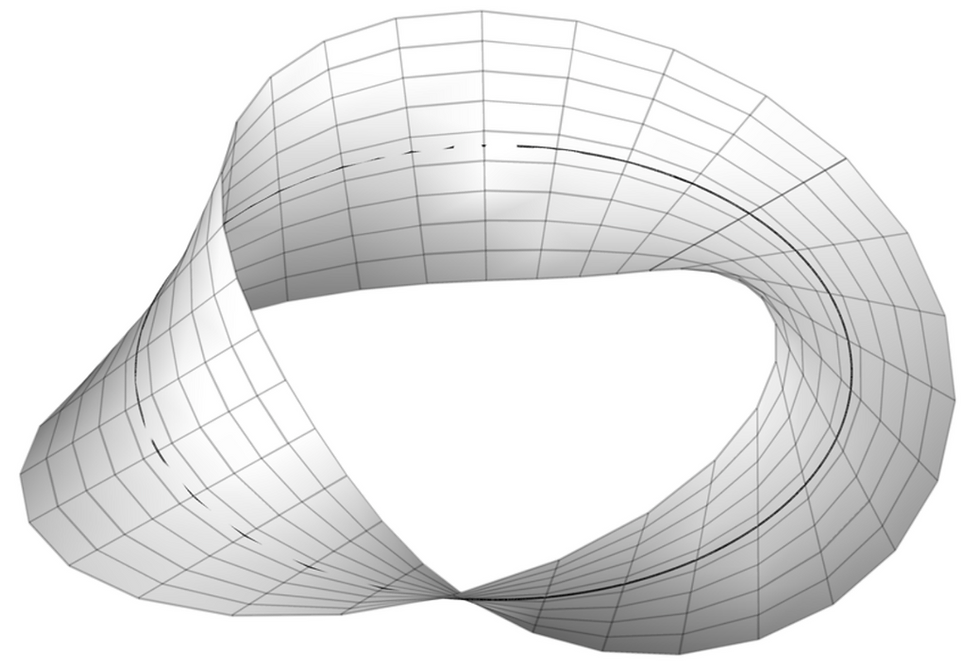
The Mobius strip is a one-sided surface with only one boundary curve. To visualize the shape of the Mobius strip, imagine taking a long narrow strip of paper and giving it a half twist before connecting the ends together to form a loop shape. It can be observed that, unlike a traditional loop, the Mobius strip only has one side and one edge. If you were to trace a path from any point along the ring, you would eventually end up where you started, having gone through both surfaces of the ring.
This character simply means that there is no method to define any edges or surfaces on the strip. There simply isn’t an inside or outside edge. Due to this property, the Mobius Strip has been studied extensively. Another example of its intriguing geometric property is that when the Mobius strip is cut lengthwise along its centerline, it results in a longer strip with two full twists rather than separate strips. This demonstrates the strip's inherent symmetry and challenges the conventional notions of division and separation in mathematics.
Works Cited
Alagappan, S. (2021). The Timeless Journey of the Möbius Strip. [online] Scientific American. Available at: https://www.scientificamerican.com/article/the-timeless-journey-of-the-moebius-strip/ [Accessed 21 Apr. 2024].
.png)

Commentaires